Resolución del Problema NP del Milenio: Eficiencia Energética mediante Transformaciones Inversas

Resumen: Este trabajo propone una solución teórica al problema NP del milenio mediante una transformación inversa que permite reducir el consumo energético computacional sin descartar combinaciones. La clave radica en representar la eficiencia algorítmica como una función inversa de la energía total consumida. Se fundamenta en principios de la termodinámica y busca ofrecer una nueva mirada sobre los límites físicos que impiden actualmente resolver este tipo de problemas.

Introducción

El problema radica en las limitaciones físicas de los sistemas de cómputo por la cantidad inmensa de datos a procesar que implican los problemas NP. Tornándose imposible de resolver, ya que no darían a basto los recursos computacionales ni las centrales de datos. Se los denomina NP porque son fáciles de validar pero difíciles de resolver óptimamente. En este trabajo propongo una formalización del concepto de eficiencia inversa en algoritmos de búsqueda sobre grafos, basándome en el análisis del consumo energético proporcional al número de combinaciones evaluadas.

Fundamentos Físicos y Computacionales

La ley de conservación de la energía (primera ley de la termodinámica) establece que la energía no se crea ni se destruye, solo se transforma. Algunas fórmulas relevantes:

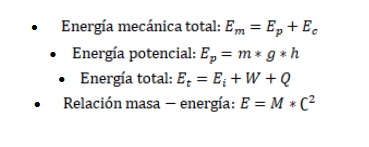
Fórmula 1

En computación, toda operación consume energía. Más operaciones implican más consumo de memoria, procesamiento y almacenamiento, y por ende, mayor demanda energética y temporal.

Modelo de Consumo Energético y Transformación Inversa

Modelo de transformación
Modelo de transformación
Modelo de transformación

Aplicando una transformación inversa..

Modelo de transformación

Aplicación a Problemas de Rutas

Supongamos un valor óptimo inverso de 0.0002 km para una ruta, pero debe reflejar respecto a un área total de 400 km², en congruencia con el sistema directo, no indirecto, entonces:

Aplicación a rutas
Este sería el trayecto más corto calculado mediante la transformación. Se parte del resultado inverso para obtener el directo mediante una regla proporcional.

Aplicación a Distribución de Estudiantes

Si 100 alumnos son distribuidos como solución óptima en una matriz de 10x10, se trata de una optimización cualitativa. No importa cuántas combinaciones de 100 cuantitativamente sean válidad, sino cuál es la mejor cualitativamente.

Considerando que, en este caso el problema implica matrices adquiere otras cualidades, ya que hay que respetar las operaciones matriciales permitidas

Se establece: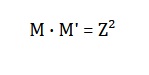

Aplicación a rutas

Donde M es la solución directa y M' la inversa. Aplicando álgebra matricial se obtiene la configuración óptima espacialmente distribuida.

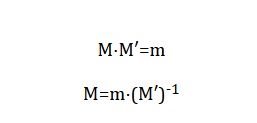
Distribución de estudiantes

Ejemplo con 400 Estudiantes y Pares Incompatibles

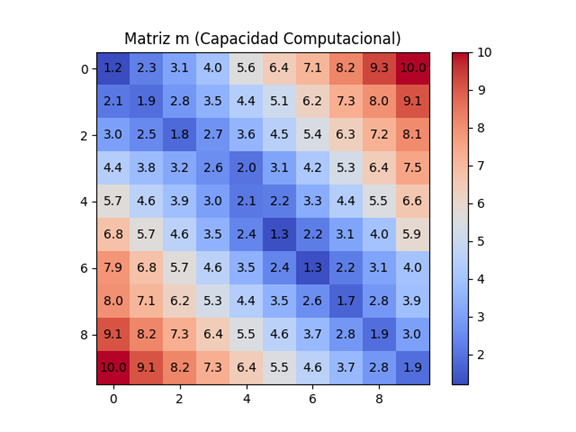
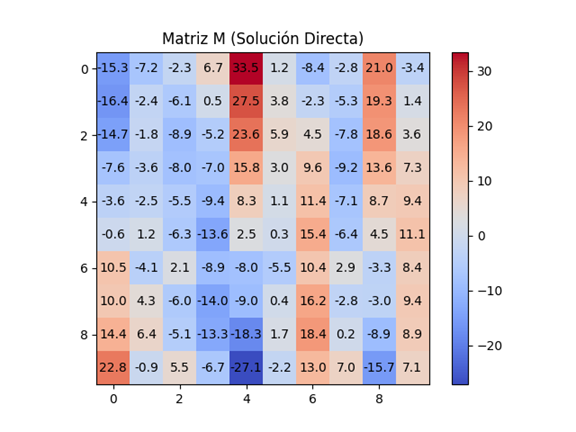
Dado un conjunto de 400 estudiantes, se desea seleccionar 100 para un único salón con capacidad exacta para ellos. Además, se debe respetar una lista de pares incompatibles provista por el director. En este contexto, cada solución de 100 alumnos puede representarse como una matriz de 10x10 (espacial y lógicamente equivalente). Se parte de una matriz mayor de 20x20, que representa la distribución global de los 400 estudiantes en bloques posibles de interacción. En esta matriz, se reflejan las zonas de incompatibilidad como valores mínimos o nulos en la matriz inversa M'. Matriz M (solución directa) y Matriz M' (solución inversa) son de 10×10, cada una representando una distribución de 100 estudiantes. La matriz Z, en cambio, es una 20×20, representando la totalidad de los 400 estudiantes y sus relaciones de compatibilidad/incompatibilidad. La matriz m que determina la capacidad computacional.

En este marco: Cada celda de Z representa la relación energética (positiva o negativa) entre subconjuntos de estudiantes. Buscar una submatriz 10×10 óptima en Z permite deducir M', y luego obtener M como su inversa cualitativa. Entonces, la clave es: "Extraer la submatriz de mayor energía compatible (sin conflictos) dentro de Z para construir M', y aplicar la transformación inversa para deducir M."

El procedimiento inverso consiste en:

  • 1. Definir Z: una matriz 20x20 que representa el campo energético inverso de las incompatibilidades.
  • 2. Determina la matriz m en función de la capacidad computacional.
  • 3. Determinar dentro de esa matriz qué submatriz 10x10 (equivalente a 100 estudiantes) posee el mayor valor energético sin contener nodos o celdas que representen incompatibilidades.
  • 4. Esa submatriz 10x10 será la selección óptima directa M, deducida desde la configuración inversa.

    • Donde: · Z (20×20) representa el universo completo de combinaciones (por ejemplo, todas las interacciones posibles entre los 400 estudiantes). · M′ (10×10) es una representación de baja resolución pero significativa, que resume bloques de Z y permite deducir zonas de menor costo/complejidad/combinación. · Luego, al resolver la ecuación M × M′ = m, encontrás M, que sería la combinación óptima directa compatible con las condiciones físicas (como capacidad computacional m). De esta forma, no se recorren combinatoriamente todas las combinaciones posibles, sino que se aprovecha la simetría y la inversión energética para deducir directamente la solución. Si Z es 20x20 y requiero transformarla en una matrinz M´ inversamente proporcional 10x10 (100 estudiantes).

    M ⋅ M′ = m

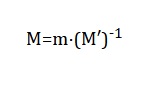
    Reducción por bloques

    Podemos reducir la complejidad computacional y representar de forma compacta los datos de 400 estudiantes situados en una dimensión abstracta, o sea en la matriz Z de dimensión 20×20, si realizamos una transformación basada en agrupamiento por bloques de 2×2. Esta técnica permite obtener una nueva matriz M′ de tamaño 10×10, donde cada elemento de M′ corresponde al promedio de un bloque 2×2 en Z. El proceso puede expresarse matemáticamente como:

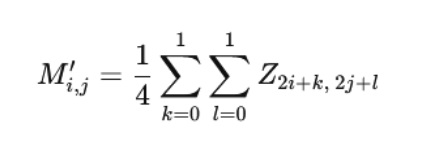
    Matriz Z

    Esta operación, aunque no es una transformación lineal clásica, puede interpretarse como un reindexado del espacio de datos, o un cambio de base no lineal, que reorganiza los elementos en subconjuntos representativos. El resultado es una matriz inversamente proporcional a la carga combinatoria, donde valores menores representan áreas con mayor densidad combinatoria en la matriz original. La reducción permite evaluar indirectamente todas las combinaciones posibles, simplificando el análisis y facilitando la comparación con otras matrices del sistema, como la matriz de capacidad computacional m, utilizada posteriormente para calcular la matriz de decisión M mediante la operación:

    En código Python:

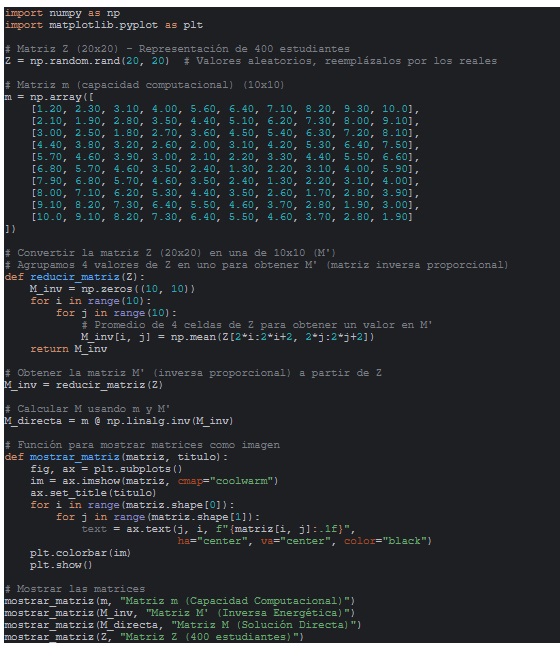
    Código Python

    Resultados:

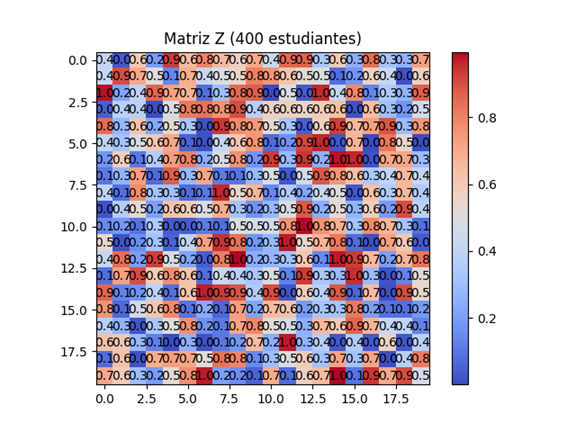
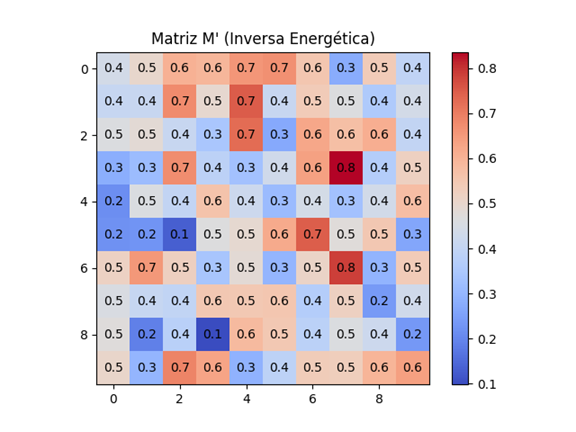
    Resultado 1 Resultado 2 Resultado 3 Resultado 4

    Conclusión

    La transformación inversa de la energía total en eficiencia unitaria permite enfrentar problemas NP con un enfoque diferente: manteniendo todas las combinaciones, pero analizándolas desde una representación energética proporcional inversa. Este método evita el descarte y propone una vía viable para deducir soluciones óptimas desde los límites físicos del sistema.

    Perspectivas Futuras

    • Desarrollo de software basado en esta lógica.
    • Extensión a problemas NP-completos clásicos.
    • Aplicación en sistemas distribuidos energéticamente eficientes.

    Autor: Maximimiliano j. Chazarreta